The answer is yes according with the following papers;
1. Keke Li, Character-valued index theorems in supersymmetric string theories; Class. Quantum Grav. 5 (1988) 95-109.
2.

In the paper 1, for the heterotic string with SO(32), the following action is used
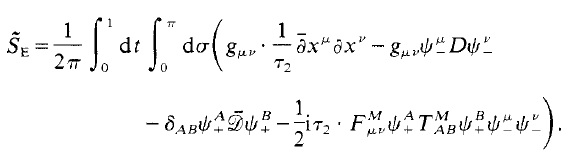
where x are bosons , psi_ are right moving fermions; and psi+ are left moving fermions.
According with paper 2 we have the following theorem

Then, combining the papers 1 and 2, it is possible to consider the heterotic string S0(32) with d = 10; as a principal fiber bundle with structure group SO(32)xSO(10). In this case the bosons and the right-moving fermions are living in the associated fiber bundle corresponding to the principal fiber bundle with structure group SO(10). The left-moving fermions are living in the associated fiber bundle corresponding to the principal fiber bundle with structure group SO(32). The bosons and the right-moving fermions are coupled to the curvature tensor for SO(10). The left.moving fermions are coupled to the Yang-Mills field for SO(32).
Do you agree?
 Q&A (4908)
Q&A (4908) Reviews (205)
Reviews (205) Meta (440)
Meta (440) Q&A (4908)
Q&A (4908) Reviews (205)
Reviews (205) Meta (440)
Meta (440)