Can anyone provide the formula for the differential cross section in square meters (sic) for Møller scattering? And maybe even give an authoritative reference?
I need the formula both for checking my math and for testing some computer programs.
I am interested in a formula which uses the International System of Units (SI) in general and m (meter), kg (kilogram), s (second) and A (Ampere) in particular.
Most sources can agree that the differential cross section in the Center of Mass (CM) coordinate system for a scattering angle θ∈(0,π) and for incomming electrons which each have momentum p∈R+ is given by
dσdΩ=β4((mc)2+2p2)2+(4p4−3((mc)2+2p2)2)(sinθ)2+p4(sinθ)4p4(sinθ)4
for some constant
β∈R+ which is measured in square meters in the SI system. Unfortunately, the sources I have found are not very explicit about
β and may even disagree with one another.
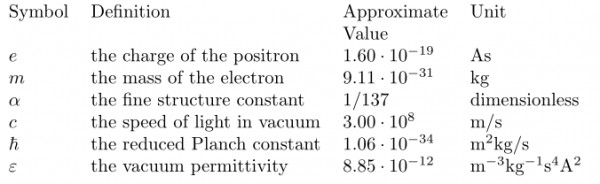
So the question is: can anyone provide a formula for β using the following physical constants?
 Q&A (4906)
Q&A (4906) Reviews (205)
Reviews (205) Meta (440)
Meta (440) Q&A (4906)
Q&A (4906) Reviews (205)
Reviews (205) Meta (440)
Meta (440)