What do people mean with a vev=diag( -2,-2,-2,-2,-2,-2,3,3,3,3)?

Question

For example, in this paper on page 21 the authors write the vev that breaks $SO(10)$ to $SU(4)\times SU(2) \times SU(2)$

$$<54>= 1/5 \cdot diag( -2,-2,-2,-2,-2,-2,3,3,3,3) \omega_s$$

where $\omega_s$ denotes the scale.

What do the authors mean by this?

The Higgs field or Higgs fields that develop a vev are elements of the $54$ representation of $SO(10)$. Because $10 \otimes 10 = 1_s \oplus 54_s \oplus45_a$, we can write each element of $54$ as a $10 \times 10$ matrix.

This is similar how one determines the particle content of the $10$ representation of $SU(5)$, written as $5 \times 5$ matrix, by using $5 \otimes 5 =10 \oplus \ldots$.

The quantum numbers of the 10 inedpendent fields $\in$ 10 are given by

$$QN(10_{ij})= QN(5_i) + QN(5_j) ,$$
where $10_{ij}$ denotes the $ij$ element of the $5 \times 5$ matrix.

This yields

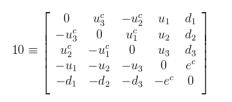
Completely equivalently we can determine the quantum numbers of the Higgs fields in the $54$ representation of $S0(10)$ and write them in a $10 \times 10$ matrix.

How does $<54>= 1/5 \cdot diag( -2,-2,-2,-2,-2,-2,3,3,3,3) \omega_s$ tell me which of these $54$ Higgs fields gets a vev?
 

---

For concreteness let's consider a simplified setup. A computation similar to $QN(10_{ij})= QN(5_i) + QN(5_j) ,$, which yields for example the 10 of $SU(5)$ as quoted above, yields a matrix for the Higgs bosons. For example, in a 2×2 case: $\begin{pmatrix} A & B  \\ C& D  \end{pmatrix}$, where $A,B,C,D$ denote four different Higgs fields. Now given a vev = diag(1,−1)w, does this mean the Higgs field A gets a vev w and the Higgs field D gets a vev −w, while C and D do not get a vev?