I am trying to do an exercise from Scattering Amplitudes By Elvang (Exercise 2.9) which states:
Show that A5(f−ˉf−ϕϕϕ)=g3[12][34]2[13][14][23][24]+3↔5+4↔5 in Yukawa theory
So, I draw the feynman diagram, which I think looks something like this (the interaction term is Li=gϕψˉψ):
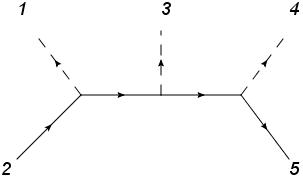
Is this diagram correct? Using the Feynman rules for Yukawa theory (in the Massless Spinor Helicity formalism) I evaluate this to be:
A5(f−ˉf−ϕϕϕ)=g3⟨2|(p1+p2)((p1+p2)2(p1+p2+p3)(p1+p2+p3)2|5⟩ + 1↔3+ 1↔4+ 3↔4
My strategy thus far has been calculate the first term then simply do the permutations at the very end. In general, is this a good strategy to take with diagrams like this?
Doing this, I end up with the following for the first term:
A(1)5=g3⟨2|s13s12(s12+s13+s23)|5⟩
Where sij=−(pi+pj)2=2pi⋅pj and I have used the Weyl equation ⟨2|p2=0.
I can go further, using the fact that sij=⟨ij⟩[ij], to end up with:
A(1)5=g3⟨2|⟨13⟩[13]⟨12⟩[12](⟨12⟩[12]+⟨13⟩[13]+⟨23⟩[23])|5⟩
I can't seem to simplify this further. Am I going the right away about solving this? Are there any tricks I am missing?
 Q&A (4905)
Q&A (4905) Reviews (206)
Reviews (206) Meta (439)
Meta (439) Q&A (4905)
Q&A (4905) Reviews (206)
Reviews (206) Meta (439)
Meta (439)