projective representation of supergroup

Question

In fact, I am not very clear about what I am asking, but I am looking for a concrete example of supergroup which has non-trivial projective representation(some supergroup similar to usual Lie group SO(3), which has $H^2(SO(3),U(1))=Z_2$ as group cohomology.)

This post imported from StackExchange MathOverflow at 2015-11-20 14:55 (UTC), posted by SE-user Yingfei Gu

Answer 1

You are asking for interesting 2-cocycles on super Lie groups which are not just 2-cocycles on the underlying bosonic Lie groups. Here is one example:

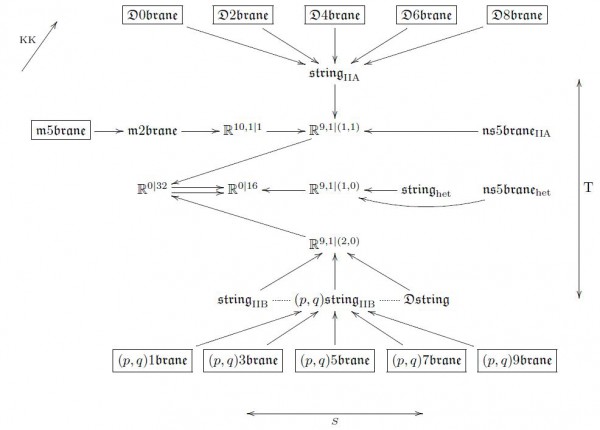
Exceptional and fermionic (p+2)-cocycles for \(p \in \mathbb{N}\) appear on super-Poincaré groups \(\mathrm{Spin}(d-1,1) \rtimes \mathbb{R}^{d-1,1\vert \mathbf{N}}\) (where \(\mathbf{N}\) denotes a choice real spinor representation) for a finite number of triples \((d,\mathbf{N},p)\). In string theory, the table of these nontrivial triples is called the brane scan since there is one such for every spacetime dimension \(d\) for supergravity with \(\mathbf{N}\)-supersymmetries in which super p-branes may propagate.

Hence the 2-cocycles correspond to 0-branes. In particular \(\mathbb{R}^{9,1\vert 16 + \overline{16}}\) (the type IIA supersymmetry super Lie group) carries such a 2-cocycle, corresponding to the D0-brane in typeII A string theory.

The corresponding projective representations are equivalently ordinary representations of the corresponding central extension. The central extension classified by the D0-brane 2-cocycle on the 10d supertranslation group is curious: it's 11d super-translation group. (This is a super Lie theoretic incarnation of the physics lore that type IIA string theory grows an 11th dimension via D0-brane condensation.)

There is loads of further interesting super Lie theoretic structure hidden in the super Lie cocycles of the brane scan. See The brane bouquet for more.