Assume a 1D Fermi gas/liquid with N electrons and a 2 body interaction: V(xi,xj)=−|g|δ(xi−xj)
The second quantization is given by:
H=∑kσϵkc†kσckσ+∫kk′qc†kσc†k′σ′V(q)ck′−q,σck+q σ
The Fourier transform of the interaction is:
V(q)=−|g|∫dx eiq(xi−xj) δ(xi−xj)=−|g|
Therefore the nth order Feynman diagram interaction in phase space is (−|g|)n.
The energy spectrum will have the correction of ∑n(−|g|)n, this sum converges for |g|<1.
1. Is it a good "classical" model for cooper pairs? I feel it doesn't because for |g|≥1 the model explodes.
2. It resembles the analogy between Landau diamagnetism and Pauli paramgnetsim. Like it's said on Pauli paramagnetism's wiki page:
The Pauli susceptibility comes from the spin interaction with the
magnetic field while the Landau susceptibility comes from the spatial
motion of the electrons and it is independent of the spin
3. Is my analysis correct at all?
4. Is this the Feynman diagram expansion (borrowed from here):
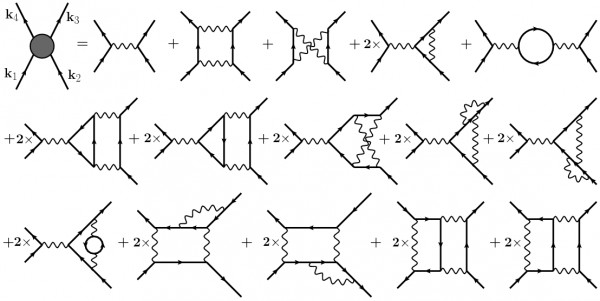
 Q&A (4912)
Q&A (4912) Reviews (205)
Reviews (205) Meta (440)
Meta (440) Q&A (4912)
Q&A (4912) Reviews (205)
Reviews (205) Meta (440)
Meta (440)