Spinors are much better and much easier understood in the older, real valued Euler Parameter representation. It has direct applications in classical mechanics and other areas.
Many essential spinor properties are hopelessly lost and obscured in the complex Cayley-Klein representation that Pauli adopted and which is generally the only representation that physicist are familiar with. As a result (quantum) physicist have an incomplete understanding of spinors.
The (real) Euler parameter representation of a SPINOR is obtained as below in such a way that 3 of the 4 elements can be directly associated with x, y and z. This already makes interpretation much simpler.
(a+ibc+id) ⟶ (abcd) ⟶ (uxyz)
The Euler parameter representation of a PAULI MATRIX and any other 2x2 complex matrix is obtained by replacing each complex element by a real valued 2x2 matrix.
a+ib ⟶ (a−bba) ∗ ⟶ (100−1)
Note that the complex conjugate operator becomes simply another real valued matrix further simplifying interpretations. Group theoretically: SU(2) combined with ∗ gives us SO(4):

Note that the colored rectangles correspond with the three SO(3) generators for x, y and z. Simplifying things again because the jx,jy,jz are in fact just the three spinor rotation generators!
The standard Pauli matrices are σ1, σ2 and σ3. The indices x, y and z in the jx,jy,jz, the ix,iy,iz and σx,σy,σz are chosen so that they correspond with the SO(3) rotation matrices.
------------------------------- The generators of local (internal) rotation -------------------------------
So the jx,jy,jz are just the standard Lorentz rotation generators. In 3D jargon: They rotate the spinor in World coordinates.
The following very important insight is completely absent from the quantum physics text books:
If we do the calculations then it turns out that the generator triplet ix,iy,iz rotates the spinor in the spinor's own, Local, coordinates. This corresponds with the rotation of ,for instance, an airplane around its Roll, Pitch and Yaw axis.
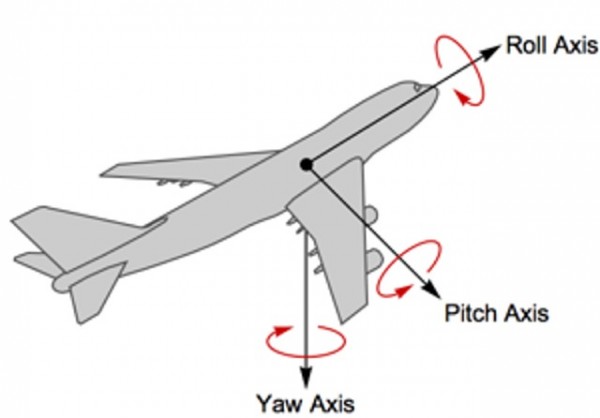
The generator that rotates the spinor around its own axis is ix (or in Pauli representation iσo)
This is well known but it is completely missed that ix is part of an anti-commuting triplet ix,iy,iz For instance iy=σ2∗ rotates a spinor 180 degrees into the opposite direction. As such this operator is generally confused with the parity operator but it is NOT a point inversion (proof: Goldstein, classical mechanics 4.5) but a relative rotation!
------------------------ The spinor base states in the real representation ------------------------
Next point generally misunderstood:A spinor represents an orientation (unlike a vector which represents merely a direction). A spinor defines a 3D local reference frame x′,y′,z′ therefore a spinor corresponds to a unique rotation matrix. We will show how to calculate this rotation matrix using only a single matrix multiplication using the two matrix triplets jx,jy,jz and ix,iy,iz
Examples: the rotation matrices belonging to the 4 base states:
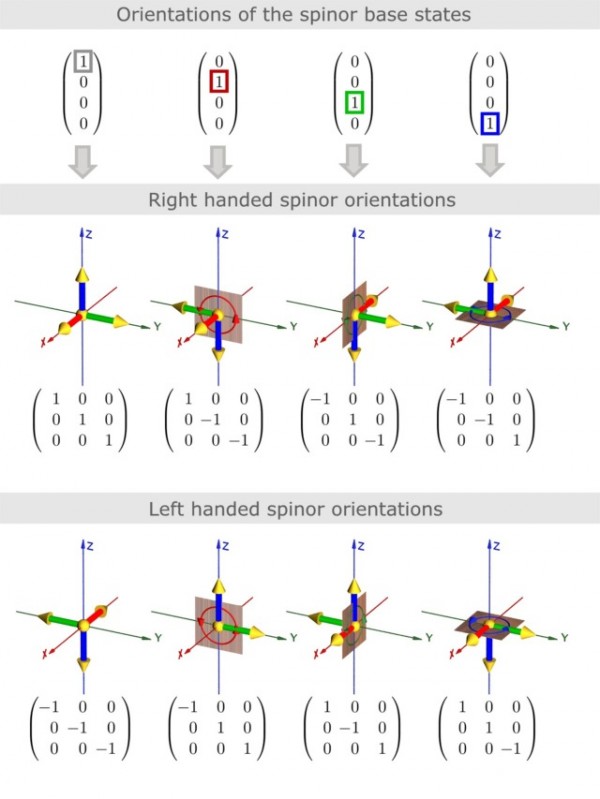
A rotation matrix is defined by three orthogonal vectors. These vectors span up the local reference frame of the spinor. The four parameters of a spinor in the real representation give us the four base states as shown in the image above.
The base state (1,0,0,0) corresponds with an orientation were the local reference frame is aligned with the coordinate axes. x'=x, y'=y, z'=z. The other base states (0,1,0,0) (0,0,1,0) and (0,0,0,1) correspond with 180o rotations around the x, y and z-axis.
Every spinor maps to a right handed local coordinate system. For left handed spinors we multiply the rotation matrix with -1 to obtain a left handed local coordinate system.
-------------------------------- The local coordinate system of a spinor --------------------------------
The following very important formula to calculate the spinor's local coordinate is completely absent from the (qantum) physics textbooks.
For an arbitrary spinor (u,x,y,z) we can calculate its local coordinate system with the following matrix multiplication:
ˇξˆξ = (ξ⋅i)(j⋅ξ) = |ξ|2(1 0 0 0 0 XxXyXz0 YxYyYz0 ZxZyZz)
With ˆξ and ˇξ written out as:
ˆξ = (ξ⋅j) = (ujo+xjx+yjy+zjz) = ( u x y z−x u−z y−y z u−x−z−y x u)ˇξ = (ξ⋅i) = (uio+xix+yiy+ziz) = ( u−x−y−z x u−z y y z u−x z−y x u)
Although the matrix multiplication is mine, the result is exactly identical to the Euler-Rodrigues formula
------------------------------------- General spinor rotation formula ---------------------------------------
We can now define a general spinor rotation formula with both matrix triplets jx,jy,jz and ix,iy,iz ( Again you won't find this formula in any textbook...)
e 12(a⋅i+b⋅j) ξ ⟶ ea⋅J(ˇξˆξ) e−b⋅J$
Where the left side operates on the spinor ξ and the right side operates on the local coordinate system ˇξˆξ and the J contain the SO(3) rotation generators. To highlight the complete independence of the histories of rotations in world coordinates and internal coordinates we can write this formula using integrals over time.
e 12∫(a(t)⋅i + b(t)⋅j)dt ξ ⟶ e+∫a(t)⋅Jdt(ˇξˆξ) e−∫b(t)⋅Jdt
-------------- Calculating the components of the precessing (spin 1/2) spinor --------------
The 3 vectors that span the local reference frame of the spinor are in fact the same as the three spin vectors sx, sy and sz while the sum of the three is the total spin s The generator ix makes the total spin precess around sx, the spinor's local x-axis. We can now actually calculate the components of this familiar image:
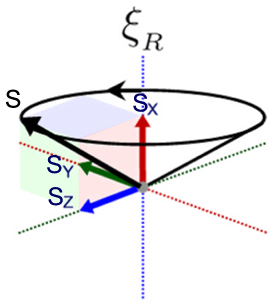
The other two generators make the total spin precess around the local y- and z-axis. Compare this with rigid body dynamics where a body can rotate around any of its three principle axes.
Where in SU(2) we have only one generation of fermions, in SO(4) we have 3 generations of fermions.
The overlooked generators iy and iz, that are nevertheless already a part of the Standard Model, can describe three different, mutually orthogonal, types of fermions. The CKM and PMNS matrices can be directly associated with this triplet of generators in order to mix generations.
See the sections 1.2, 1.3 and 1.4 of chapter 1 and the whole of chapter 2 here:
To see how QED (1 boson field, 1 fermion generation) can be perfectly extended to the full Electroweak Theory (extra boson triplet and 3 fermion generations) see here: https://thephysicsquest.blogspot.com/
 Q&A (4906)
Q&A (4906) Reviews (205)
Reviews (205) Meta (440)
Meta (440) Q&A (4906)
Q&A (4906) Reviews (205)
Reviews (205) Meta (440)
Meta (440)