Question and Summary
Using classical calculations and the Robin boundary condition I show that one calculate the anti-derivative of a function within time $2X$ I can compute an integral
$$\frac{2 \alpha}{\beta} e^{ \frac{\alpha}{\beta}X} \int_0^{X} e^{- \frac{\alpha}{\beta}\tau} \tilde f_0(\tau) d \tau$$
where $f_0$ is an arbitrary function whose integral above converges.
I believe for reasons mentioned below this should not be possible and is only an approximation when the quantum properties of the boundary are not taken into consideration. I would like to know if it is plausible using the arguments below?
Background
Let us assume the Minkowski Half-spacetime in $1+1$ dimensions with a Robin boundary condition as the $t$ axis which satisfies $\alpha \Phi(x,t)|_{x=0} + \beta \partial_x\Phi(x,t)|_{x=0} = 0$ where $\alpha$, $\beta$ are numbers and $\Phi$ is the field.
d'Alembert's Formula
The light cone coordinates are
$$x^\pm = \frac{1}{\sqrt 2} (t \pm x)$$
The solution to the Klein-Gordon Equation is
$$\Phi(x^+,x^-) =\frac{1}{2}\Big(f_0(-\sqrt 2 x^-) + f_0(\sqrt 2 x^+) + \int_{-\sqrt 2 x^-}^{\sqrt 2 x^+} f_1(z) dz \Big) $$
Where:
$$\Phi|_{t=0}= f_0(x) $$
and
$$ \partial_t \Phi|_{t=0}= f_1(x) $$
As this satisfies
$$\square \Phi = (-\partial_t^2 + \partial_x^2) \Phi(t,x) = -2\partial_{x^+}\partial_{x^-}\Phi (x^+,x^-) = 0$$
Field Extension of Robin Condition
The Robin boundary condition is given by $\alpha \Phi|_{\partial M} + \beta \nabla_n \Phi|_{\partial M} = 0$.
$$\frac{\alpha}{2}\Big(\tilde f_0(t) + \tilde f_0(-t) + \int_{-t}^{t} \tilde f_1(z) dz\Big) + \frac{ \beta}{2}\left ( \tilde f_0'(-t) + \tilde f_0'(t) - \tilde f_1(-t)+ \tilde f_1(t) \right ) = 0$$
Rearranging the equation and we can write $f_0(t)$ as the sum odd and even function:
$$\Big( \frac{\alpha}{2}(\tilde f_0(t) + \tilde f_0(-t) \Big) + \frac{ \beta}{2} \Big(\tilde f_0'(-t) + \tilde f_0'(t) \Big) + \Big( \frac{\alpha}{2} \int_{-t}^{t} \tilde f_1(z) dz + \frac{ \beta}{2} (\tilde f_1(t)- \tilde f_1(-t))\Big) = 0$$
Applying the trick that the sum of an even and an odd function can only be $0$ when the functions are independently $0$.
$$\frac{\alpha}{2}(\tilde f_0(t) + \tilde f_0(-t) ) + \frac{ \beta}{2} (\tilde f_0'(-t) + \tilde f_0'(t)) =0$$$$\frac{\alpha}{2} \int_{-t}^{t} \tilde f_1(z) dz + \frac{ \beta}{2} (\tilde f_1(t)- \tilde f_1(-t))= 0$$
Differential equations express the local properties of functions. However, if we wish to think globally and know only the functions in the Half space then Equations above are not so useful. Hence, we proceed to find the global functions. A detailed analysis using Laplace transforms yields:
$$\tilde f_0(-t) = \tilde f_0(t) - \frac{2 \alpha}{\beta} \int_0^{-t} e^{- \frac{\alpha}{\beta}( -t -\tau)} \tilde f_0(-\tau) d \tau$$
Thus if one knows the value of $f_0(t)$ for all positive $t$ then one can infer it for all negative $t$ as well from the above Equation.
Using the Boundary as a computer
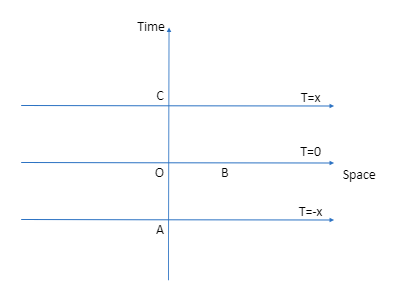
Now that we have the field extensions we can use Cauchy hyper surfaces. In particular
where there are $3$ Cauchy surfaces at time $t= 0$, $t=X$ and $t=-X$.
Consider the value of the fields at the points
$$\Phi(x,t)|_{(t=-X,x =0)} = \frac{1}{2}\Big(\tilde f_0(-X) + \tilde f_0(X) + \int_{-X}^{X} \tilde f_1(z) dz\Big) = 0$$
$$ \Phi(x,t)|_{(t=0,x =X)} = f_0 (X)$$
$$\Phi(x,t)|_{(t=X,x =0)} = \frac{1}{2}\Big(\tilde f_0(X) + \tilde f_0(-X) + \int_{X}^{-X} \tilde f_1(z) dz\Big) = 0$$
An observer sits at $A$ and measures $\Phi(x,t)|_{(t=-X,x =0)}$. Let us say there is another observer on $B$ who measures $\Phi(x,t)|_{(t=0,x =X)}$ and transmits this information to the observer sitting on $C$ who also measures $\Phi(x,t)|_{(t=X,x =0)}$. The observer on $C$ now makes the following calculation:
$$ \Phi(x,t)|_{(t=0,x =X)} + \Phi(x,t)|_{(t=-X,x =0)} -2 \Phi(x,t)|_{(t=0,x =X)} $$
$$=f(-X) - f(X) = \frac{2 \alpha}{\beta} e^{ \frac{\alpha}{\beta}X} \int_0^{X} e^{- \frac{\alpha}{\beta}\tau} \tilde f_0(\tau) d \tau$$
Who is faster at solving the integral Observer $C$ or $B$?
$B$ measures $\Phi(x,t)|_{(t=0,x =X)} = f_0 (X)$ and proceeds to integrate using "some algorithm" to find
$$\frac{2 \alpha}{\beta} e^{ \frac{\alpha}{\beta}X} \int_0^{X} e^{- \frac{\alpha}{\beta}\tau} \tilde f_0(\tau) d \tau$$
Observer $C$ simply uses a subtraction algorithm
$$ \Phi(x,t)|_{(t=0,x =X)} + \Phi(x,t)|_{(t=-X,x =0)} -2 \Phi(x,t)|_{(t=0,x =X)} $$
While the observer $B$ does have a lead-start of time $X$. The subtraction algorithm is far superior in computation speed and for complicated than the "some algorithm". Thus I would expect $C$ to win for most functions of $f_0$.
The real problem
There is no all purpose "some algorithm" or quantum/classical algorithm to exact compute the integral. **This leads to the question how does the boundary compute the answer so fast?**
My attempt: A possible sketchy resolution?
I thus, think a simple resolution of the paradox is that the boundary is performing the computation numeric integration in the interval $0$ to $X$ and is made almost readily available upon inferring the field at $C$. Of course this, is rather very speculative by simply looking at classical fields I seem to be making a comment on how the boundary should behave on a quantum level.
Edit:The previous line is a unfair as even if one quantizes the (Massless Inhomogeneous) Klein-Gordon field by making the following substitution:
$$ f_0(x) \to h_0(x) = f_0(x) + \Big( \int^{-\frac{x}{\sqrt 2}}_{-\infty} \int^{\frac{x}{\sqrt 2}}_{-\infty} \frac{ j(z^+,z^-) dz^+ dz^-}{2}\Big ) $$
$$ f_1(x) \to h_1(x) = f_1(x) +\frac{1}{\sqrt 2} \Big( \int^{-\frac{x}{\sqrt 2}}_{-\infty} \frac{ j(\frac{x}{\sqrt 2},z^-) dz^-}{2} + \int^{\frac{x}{\sqrt 2}}_{-\infty} \frac{ j(z^+,-\frac{x}{\sqrt 2}) dz^+ }{2}\Big) $$
Where $j$ is the source ... I think the whole argument almost still holds (including my possible resolution that the boundary too must have "quantum properties")
Q&A (4870)
