How do one find out the first order correction to total cross section?

Question

I have a lagrangian $\mathcal{L}=\mathcal{L_0+\mathcal{L_1}}$, where $\mathcal{L_1}$ is a perturbation given by:$$\mathcal{L_1}=-1/3! \lambda \phi^3-1/4! \lambda \phi^4 $$
and$$\mathcal{L_0}=-\frac{1}{2}\partial^\mu\phi\partial_\mu\phi+\frac{1}{2}m\phi^2$$If I am to calculate the dominent term for the scattering amplitude and scattering cross section for the scattering $\phi\phi\rightarrow\phi\phi$,
It is straight forward.
Since the leading term for scattering amplitude should contain the least possible $\lambda$, the only possible number is one. Hence the only contribution to the scattering amplitude is the Feynman diagram given below, which contains only one vertex that is from $\phi^4$ term:

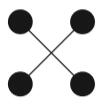
Now, here comes my question:
If I were to calculate the first correction to the leading order of scattering amplitude, we should consider all possible diagrams with 2 vertices. That is, we have to add all the diagrams containing 2 vertices from $\phi^3$ + 2 vertices diagrams from $\phi^4$ + diagrams which have one 3-vertex and one 4-vertex.

If now I want to calculate the total cross section.
It is possible that the first correction order of $\lambda$ is higher than $\lambda^2$ since some diagrams can cancel each other. How do one find out of which order in $\lambda$ is the first correction to the total cross section? Is there any simple way in this case without going through calculating all possible diagrams of order $\lambda^2$ or higer?