Asymptotic disperson of 2D wave equation with 1D periodic potential

Question

Consider the following 2D wave equation: 

$$\left(\frac{d^2}{dx^2}-k_y^2+\omega^2\ V(x)\right)\psi(x)=0$$
where $V(x+L)=V(x)>0$ is a positive periodic potential, $k_y$ is the wave vector along $y$-direction, $\omega$ is the frequency, and the eigenfunction satisfies the periodic boundary condition $\psi(x+L)=\psi(x)$, $\frac{d}{dx}\psi(x+L)=\frac{d}{dx}\psi(x)$.

From the numerical solutions of several different periodic potentials $V(x)$, I find that all bands approach to linear asymptotic dispersion $\omega_n(k_y)$ as $k_y\rightarrow\infty$. And it seems that the asymptotic group velocities for different bands are identical and are only determined by the maximum of the potential $V(x)$, namely

$$\lim_{k_y\rightarrow\infty}\frac{d\omega_n}{dk_y}=1/\sqrt{V_{\mathrm{max}}}.$$

The following figures show two examples (the first 9 bands in each case). However, I cannot prove this conjecture. Can some one help me prove or disprove this conjecture?

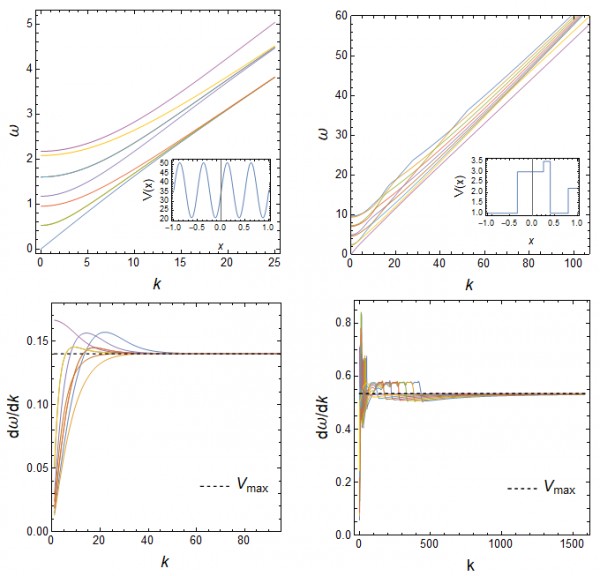
The insets in the upper subfigures are the profiles of the potential function $V(x)$ in one period.