Experimental boundaries for size of electron?

Question

There is some confidence that electron is a perfect point e.g. to simplify QFT calculations. However, searching for experimental evidence, e.g. Wikipedia article only points argument based on g-factor being close to 2: Dehmelt's 1988 paper extrapolating from proton and triton behavior that RMS (root mean square) radius for particles composed of 3 fermions should be $\approx g-2$:

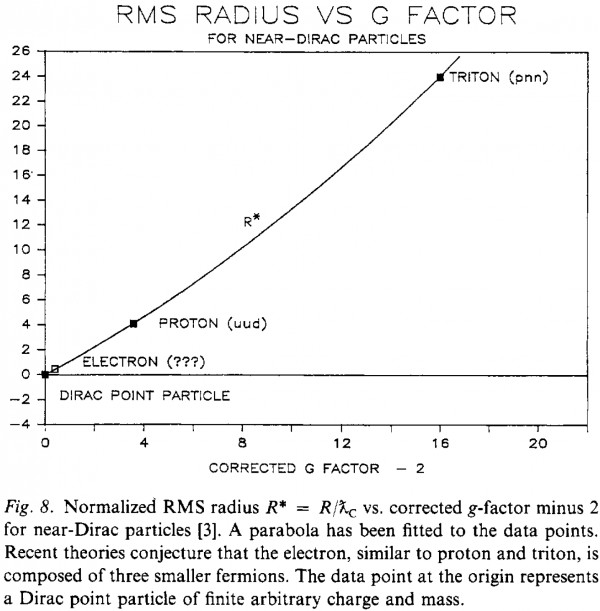
Using more than two points for fitting this parabola it wouldn't look so great, e.g. neutron (udd) has $g\approx-3.8$ and $<r^2_n>\approx -0.1 fm^2$.

And while classically $g$-factor is said to be 1 for rotating object, it is for assuming equal mass and charge density ($\rho_m\propto\rho_q$). Generally we can classically get any $g$ by modifying charge-mass distribution:

$$g=\frac{2m}{q} \frac{\mu}{L}=\frac{2m}{q} \frac{\int AdI}{\omega I}=\frac{2m}{q} \frac{\int \pi r^2 \rho_q(r)\frac{\omega}{2\pi} dr}{\omega I}=
\frac{m}{q}\frac{\int \rho_q(r) r^2 dr}{\int \rho_m(r) r^2 dr}$$

Another argument for point nature of electron is tiny cross-section, so let's look at it for electron-positron collisions: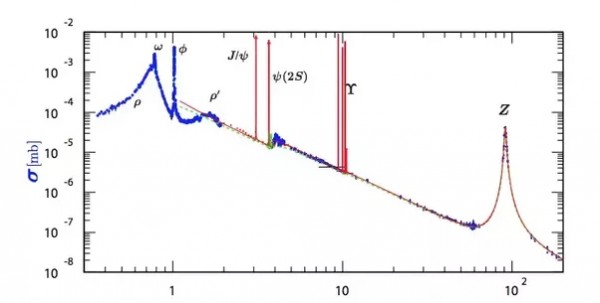

Beside some bumps corresponding to resonances, we see a linear trend in this log-log plot: $\approx 10^{-6}$ mb for 10GeVs (5GeV per lepton), $\approx 10^{-4}$ mb for 1GeV. The 1GeV case means $\gamma\approx 1000$, which is also in Lorentz contraction: geometrically means $\gamma$ times reduction of size, hence $\gamma^2$ times reduction of cross-section - exactly as in this line on log-log scale plot.

More proper explanation is that it is for collision - transforming to frame of reference where one particle rests, we get $\gamma\to\approx \gamma^2$. This asymptotic $\sigma \propto 1/E^2$ behavior in colliders is well known (e.g. (10) here) - wanting size of resting electron, we need to take it from GeVs to $E=2\cdot 511$keVs.

Extrapolating this line (no resonances) to resting electron ($\gamma=1$), we get $\approx 100$ mb, corresponding to $\approx 2$ fm radius.

From the other side we know that two EM photons having 2 x 511keV energy can create electron-positron pair, hence energy conservation doesn't allow electric field of electron to exceed 511keV energy, what requires some its deformation in femtometer scale from $E\propto 1/r^2$:

$$\int_{1.4fm}^\infty \frac{1}{2} |E|^2 4\pi r^2 dr\approx 511keV$$

Could anybody elaborate on concluding upper bound for electron radius from g-factor itself, or point different experimental boundary?

Does it forbid electron's parton structure: being "composed of three smaller fermions" as Dehmelt writes? Does it also forbid some deformation/regularization of electric field to a finite energy?

Comments

My paper here might be helpful to you.

---

Dear Vladimir, briefly looking I don't see answer to the question of focus here. Also for others, knowing such experimental evidence for electron size, please briefly specify: which experiment, how it provides boundary for electron size, and how large this boundary is.

---

Yes, my paper answers your question. In fact there are different definitions of size. If you mean the elastic picture, the size of a free electron is infinity.

Answer 1

''Could anybody elaborate on concluding upper bound for electron radius from g-factor itself, or point different experimental boundary?''

See the item ''Are electrons pointlike/structureless?'' from Chapter B2: Photons and Electrons of my Theoetical Physics FAQ. The experimental upper bound of the electron charge radius seems to be ~ 10^{-16} cm. (a 1982 figure); the 2019 listing of the particle data group doesn't give a value.

''Does it forbid electron's parton structure: being "composed of three smaller fermions"''

No. This depends on the assumed properties and interactions of the Preons making up the electron.

''Does it also forbid some deformation/regularization of electric field to a finite energy?''

Yes, since there the form factors enter, which are not those of a point particle.

Comments

Could you maybe elaborate on this 10^-16 cm bound? In your webpage there is a paper with damaged link and missing thesis.

Regarding possibility of deformation of electric field of point charge to finite energy you say is forbidden, we can create electron-positron from 2x511keV EM energy - so where does the remaining of this infinite energy of electric field comes from?

Also, running coupling says that alpha deforms e.g. to ~1/127 for 90GeV collisions - would such deformation be needed for perfect point charges?

---

@Jarek: I corrected the link. I don't know more about the matter than is listed in my FAQ. In any case, the electron is definitely not a point, only pointlike.