In order to answer this we need to develop some concepts first. I will touch on some of the issues with the black hole firewall paradox, but will not be addressing directly.
Preliminary
There are some statements made by Maldacena and Susskind in there paper and briefs that we will discuss [1][2][4]:
- There is some CPT [5] operation that can change the |En⟩L⊗|En⟩R basis for an entangled eternal black hole into a |En⟩CPTL⊗|En⟩R basis for states describing two black holes
- There is some process like pair production in a magnetic field that produces entangled extremal black hole pairs (where charge energy equals mass energy[6])
- The |En⟩CPTL⊗|En⟩R basis can also be used to describe the extremal pair case
This is important because one can build a pseudo-Feynman diagram of the reverse situation. If you start off with a diagram that shows the production of a extremal black hole pair derived from the diagram of a normal electron pair production in a magnetic field [8], you might draw something like:
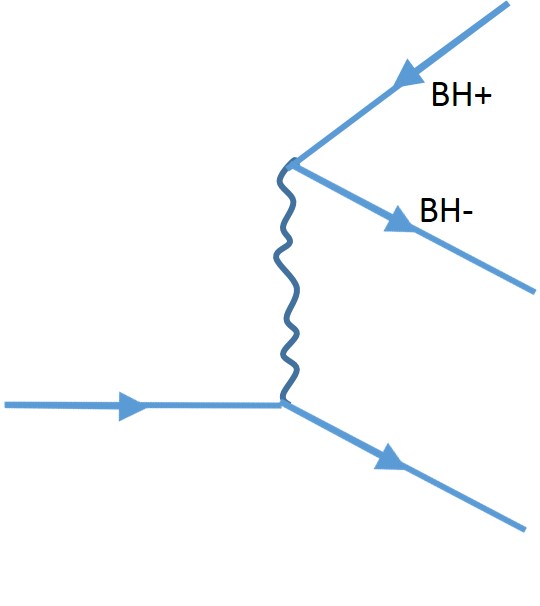
Where we label the two pairs as positive(anti-) and negative charge black holes.
If we were to perform a CPT operation on just the negative charge blackhole, we would basically change the outgoing particle into an positive charged incoming particle
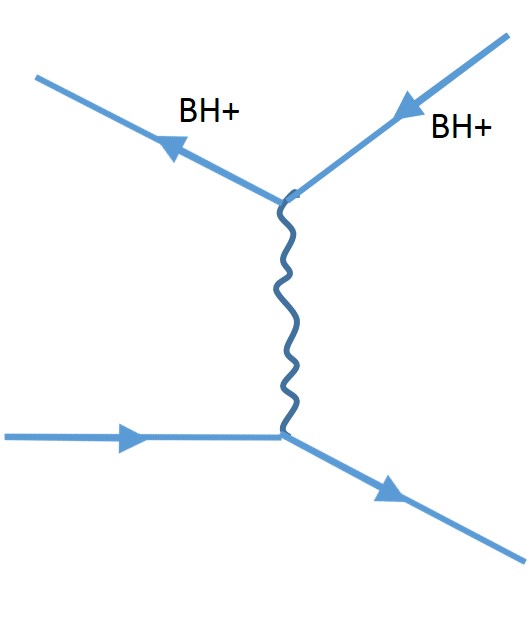
One can imagine this is akin to changing the entangled system state from:
|Ψ⟩=∑ne−βEn/2|En⟩CPTL⊗|En⟩R
to the entangled state of the eternal black hole[1]:
|Ψ⟩=∑ne−βEn/2|En⟩L⊗|En⟩R
The implication is that one has changed a pair production amplitude into a scattering amplitude. The connection is because the above states are bipartite entanglement states that are produced via an interaction Hamiltonian [9][10], which governs the time evolution of states [11], which in the case described by Maldacena and Susskind is described by [1]:
|Ψ(t)⟩=∑ne−βEn/2e−2iEnt|En⟩CPTL⊗|En⟩R
Time Travel interpretation
The physics regarding time travel for an eternal black hole in the conventional sense is actually well explained in Chapter 30 of Roger Penrose's book The Road to Reality [12]. If one wanted to, they could interpret time travel as being a situation where a negative energy real particle escaped from a black hole as a tachyon. This is of course an unphysical situation, although tachyons come up in discussion of loop self-energy, the absence of tachyons is a key supporting factor for supersymmetric string theories [13].
The question from an entanglement point of view might be whether there can be a backwards propagating entanglement between particles? Or rather, can two particle that are space-like separated at creation from independent non-interacting systems be entangled before a time-like interaction?
In this situation, the proper statement would seem to be:
Time Travel = Superluminal pre-entanglement
Or in other words, one cannot backwards evolve a simple product state |ψS⟩=|ψA⟩⊗|ψB⟩ into an entangled state. This is enforced in quantum field theory by locality requirements which manifest themselves by requiring that operators commute if they are outside each other light cone [14].
Comments on the Firewall
The principle concern of the firewall paradox is how to get information out of the black hole [7]. Polchinski uses the analogy of breaking a chemical bond in order to get the information out of the black hole. In a traditional view, an infalling observer does not see a firewall, but rather a rapidly redshfting image of the collapsing matter that formed the black hole [15]. The need to resort to firewalls seems to be extreme, especially if the entangled copies are separated by an infinite potential. This is the starting point for discussions for computational complexity relationship to black holes [16].
[1] Cool horizons for entangled black holes
Juan Maldacena (Princeton, Inst. Advanced Study), Leonard Susskind (Stanford U., ITP & Stanford U., Phys. Dept.). Jun 3, 2013. 31 pp.
Published in Fortsch.Phys. 61 (2013) 781-811
DOI: 10.1002/prop.201300020
[2] Maldacena, J (2013), Wormholes and entangled states, http://online.kitp.ucsb.edu/online/fuzzorfire_m13/maldacena/pdf/Maldacena_FuzzOrFire13_KITP.pdf
[3] Black Holes: Complementarity or Firewalls?
Ahmed Almheiri (UC, Santa Barbara), Donald Marolf (UC, Santa Barbara & Santa Barbara, KITP), Joseph Polchinski (Santa Barbara, KITP), James Sully (UC, Santa Barbara). Jul 2012. 23 pp.
Published in JHEP 1302 (2013) 062
DOI: 10.1007/JHEP02(2013)062
[4] Maldecena, A.(2013),Wormholes and entangled states, Strings 2013,
[5] Kleis, R.,(2013), Pictures, Paths, Particles, Processes, http://www.hef.ru.nl/~kleiss/qft.pdf
[6] Hamilton, A (2014) Penrose Diagrams, http://jila.colorado.edu/~ajsh/insidebh/penrose.html
[7] Polchinski, J (2013) Black Holes and Firewalls-SETI Talks,
[8] Novak,P. Kholodov,R.I.(2012) Electron-positron pair production by an electron in a magnetic field in the resonant case, http://arxiv.org/abs/arXiv:1210.6189
[9] Haroche, S., Raimond, J.M., (2006), Exploring the Quantum, http://www.amazon.com/Exploring-Quantum-Cavities-Photons-Graduate/dp/0198509146
[10] Yavari, N (2001) The Hamiltonian of Interaction, http://web.ift.uib.no/AMOS/nazila/LaserAndLight/node5.html
[11] McMahon, D., (2008) Quantum Field Theory DeMystified, http://www.amazon.com/Quantum-Field-Theory-Demystified-McMahon/dp/0071543821
[12] Penrose, R., (2004), the Road to Reality, http://www.amazon.com/The-Road-Reality-Complete-Universe/dp/0679776311
[13] unknown (2014), Tachyon, http://universe-review.ca/R15-28-tachyon.htm#physics
[14] Veltman, M. (1994). Diagrammatica: The path to Feynman rules. Cambridge: Cambridge University Press.
[15] Einstein,A. (2014) Relativity and Gravitation: 100 Years After Einstein in Prague, http://books.google.com/books?id=6KnIAwAAQBAJ&pg=PA100&lpg=PA100&dq=Penrose+diagram+of+the+complete,+analytically+extended+Schwarzschild+geometry&source=bl&ots=MW7w8w8Ewy&sig=VHvkpz-I3cGQKkD5ZpZ3efRY3Dc&hl=en&sa=X&ei=-uBwVIDhAobbsASww4Fw&ved=0CC4Q6AEwAg#v=onepage&q=Penrose%20diagram%20of%20the%20complete%2C%20analytically%20extended%20Schwarzschild%20geometry&f=false
[16] Susskind, L. (2014) Computational Complexity and Black Hole Horizons http://arxiv.org/abs/1402.5674
 Q&A (4912)
Q&A (4912) Reviews (205)
Reviews (205) Meta (440)
Meta (440) Q&A (4912)
Q&A (4912) Reviews (205)
Reviews (205) Meta (440)
Meta (440)