6j symbols with Majorana indices

Question

The Levin-Wen model is a Hamiltonian formulation of Turaev-Viro (2 + 1)d TQFTs. It can be constructed from a unitary fusion category $\mathcal{C}$, which can be equivalently defined using $6j$ symbols: An equivalence class of solutions of the pentagon equation satisfying certain normalizations. 

Gu, Wen, Wang proposed a generalization of the above construction in http://arxiv.org/abs/1010.1517. The mathematical framework for such a generalization is the theory of enriched categories. By considering special enriched categories, the so-called *projective super fusion categories*, which are enriched categories over the category of super Hilbert spaces up to projective even unitary transformations, one can get a Hamiltonian formulation of the fermionic Turaev-Viro TQFTs. The *projective super fusion category* can be equivalently defined in terms of the fermionic $6j$ symbols $F^{ijm,\alpha\beta}_{knt,\eta\varphi}$, which are solutions of the fermionic pentagon equation below:

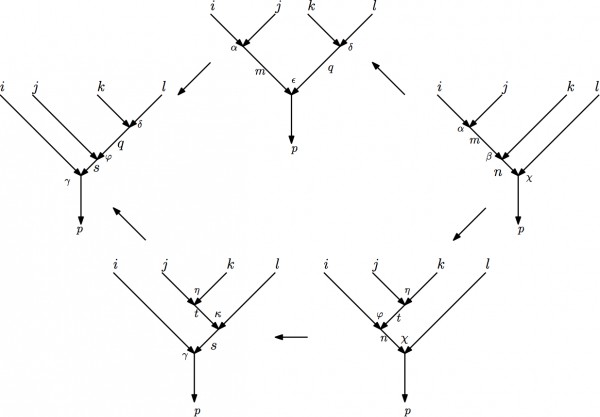
\begin{align}
&
\sum_{t}
\sum_{\eta=1}^{N^{jk}_{t}}
\sum_{\varphi=1}^{N^{it}_{n}}
\sum_{\kappa=1}^{N^{tl}_{s}}
F^{ijm,\alpha\beta}_{knt,\eta\varphi}
F^{itn,\varphi\chi}_{lps,\kappa\gamma}
F^{jkt,\eta\kappa}_{lsq,\delta\varphi}
=
(-)^{s^{ij}_{m}(\alpha) s^{kl}_{q}(\delta)}
\sum_{\epsilon=1}^{N^{mq}_{p}}
F^{mkn,\beta\chi}_{lpq,\delta\epsilon}
F^{ijm,\alpha\epsilon}_{qps,\varphi\gamma},
\end{align}
where we use English letters (bosonic indices) to label states on the edges, Greek letters (fermionic indices) to label states on the vertex. $s^{ij}_{m}(\alpha)$ is used to denote the fermion parity of the state $\alpha$.

I'd like to know if there are generalizations of the Levin-Wen model in which the relevant enriched category is defined in terms of the "Majorana $6j$ symbols $F^{ijm,\alpha\beta}_{knt,\eta\varphi}$", where there could be a single Majorana fermion sitting on the vertices. In this case, one should allow the fermion number on each vertex to fluctuate, and the Greek indices $\alpha,\beta,\eta,\varphi$ labeling the vertex states should be Majorana variables. Naturally, these "Majorana $6j$ symbols" should be solutions of a "Majorana pentagon equation".