Your question is central to my research interests, in the sense that completing that research would necessarily let me give you a precise, unambiguous answer. So I can only give you an imprecise, hand-wavy one. I'll write down the punchline, then work backwards.
Punchline: The instantaneous rate of branching, as measured in entropy/time (e.g., bits/s), is given by the sum of all positive Lyapunov exponents for all non-thermalized degrees of freedom.
Most of the vagueness in this claim comes from defining/identifying degree of freedom that have thermalized, and dealing with cases of partial/incomplete thermalization; these problems exists classically.
Elaboration: Your question postulates that the macroscopic system starts in a quantum state corresponding to some comprehensible classical configuration, i.e., the system is initially in a quantum state whose Wigner function is localized around some classical point in phase space. The Lyapunov exponents (units: inverse time) are a set of local quantities, each associated with a particular orthogonal direction in phase space. They give the rate at which local trajectories diverge, and they (and their associated directions) vary from point to point in phase space.
Lyapunov exponents are defined by the linearized dynamics around a point, and therefore they are constant on scales smaller than the third derivative of the potential. (Perfectly linear dynamics are governed by a quadradic Hamiltonian and hence a vanishing third derivative.) So if your Wigner function for the relevant degree of freedom is confined to a region smaller than this scale, it has a single well-defined set of Lyapunov exponents.
On the other hand, the Wigner function for degrees of freedom that are completely thermalized is confined only by the submanifold associated with values of conserved quantities like the energy; within this submanifold, the Wigner function is spread over scales larger than the linearization neighborhood and hence is not quasi-classical.
As mentioned above, I don't know how to think about degree of freedom which are neither fully thermalized nor confined within the linear neighborhoods.
Argument: We want to associate (a) the rate at which nearby classical trajectories diverge with (b) the production of quantum entanglement entropy. The close relationship between these two has been shown in a bunch of toy models. For instance, see the many nice cites in the introduction of
Asplund and Berenstein, "Entanglement entropy converges to classical entropy around periodic orbits", (2015). arXiv:1503.04857.
especially this paper by my former advisor
Zurek and Paz,"Quantum chaos: a decoherent definition", Physica D 83, 300 (1995). arXiv:quant-ph/9502029.
The very crude picture is as follows. An initially pure quantum state with Wigner function localized around a classical point in phase space will spread to much larger phase-space scales at a rate given the Lyapunov exponent. The couplings between systems and environments are smooth functions of the phase space coordinates (i.e., environments monitor/measure some combination of the system's x's and p's, but not arbitrary superpositions thereof), and the decoherence rate between two values of a coordinate is an increasing function of the difference. Once the Wigner function is spread over a sufficient distance in phase space, it will start to decohere into an incoherent mixture of branches, each of which are localized in phase space. See, for instance, Fig. 1 in Zurek & Paz:
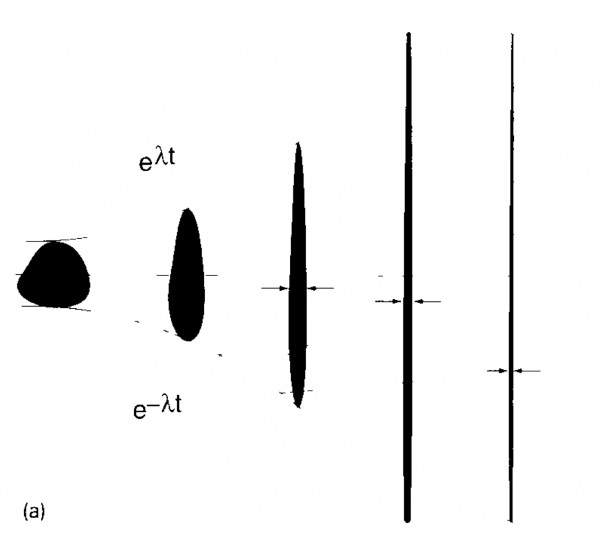
Hence, the rate of trajectory divergence gives the rate of branching.
With regard to this:
But if the person has an alarm clock triggered by nuclear decay, there may well be 50/50 branching in which the person is awake or asleep. (Note that you couldn't get such branching with a regular alarm clock.)
It's true you couldn't get such branching with a highly-reliable deterministic alarm clock, but you could dispense with the nuclear decay by measuring any macroscopic chaotic degree of freedom on a timescales longer than the associated Lyapunov time constant. In particular, measuring thermal fluctuations of just about anything should be sufficient.
One more thing (rather controversial): The reason this questions was so hard to even formulate is two fold:
- No one has a good definition of what a branch, nor how to extract predictions for macroscopic observations directly from a general unitarily evolving wavefunction of the universe. (My preferred formulation of this is Kent's set selection problem in the consistent histories framework.)
- Branching is intimately connected to the process of thermalization. Although some recent progress in non-equilibrium thermodynamics has been made for systems near equilibrium (especially Crooks Fluctuation Theorem and related work), folks are still very confused about the process of thermalization even classically. See, for instance, the amazingly open question of deriving Fourier's law from microscopic first principles, a very special case!
 Q&A (4871)
Q&A (4871) Reviews (203)
Reviews (203) Meta (439)
Meta (439) Q&A (4871)
Q&A (4871) Reviews (203)
Reviews (203) Meta (439)
Meta (439)