Defining Thermodynamic beta in dimension of time and temperature in dimension of frequency

Question

If I define Thermodynamic beta in unit of second. Does this mean that:

1. Boltzmann constant $k$ is unit-less?
2. $T$ is in units of frequency (Hz) or Kelvin $K$?

In this case, is defining Thermodynamic beta $\beta$ in unit of second a reason to make $\hbar$ unitless? To make $\hbar$ = 1 with no unit, which originally is $1.0545718 × 10^{-34} m^2 kg s^{-1}$, should Boltzmann constant $k$ be scaled appropriately?

This is the table of Student Friendly Quantum Field Theory and what I mentioned seems to belong to the hybrid case:

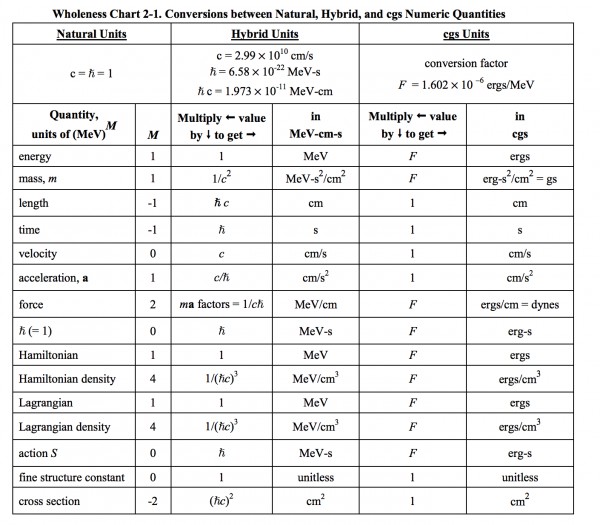
β=1/kT has the units of $J^{−1}$, so ℏβ has the units of s. Redefining a scaled version of the Boltzmann constant by 1/k′=ℏ/k  would give β′=1/k′T the units of s. However, when most of the time I would use ℏ independent of thermodynamic beta and vice versa. If I use ℏ=1, which is the cause of every scaling, setting k′=k/ℏ does work when ℏ and β is used together. But in classical statistical mechanics, no ℏ appears and β is used independently, why should β changed just because I want to set ℏ=1 unitless? 

Comments

Voting to close as not graduate-level