The Kerr-Newman metric describes a rotating charged black hole when
q2+a2<m2
where q is the charge, m is the mass and a = J/m is the angular momentum per mass, in units where G = c = 1. There are various imaginable notions of the "size" of this black hole, since there is a "stationary limit surface" within which a particle cannot stay at rest relative to the fixed stars, and then a region called the "ergosphere", then an event horizon called the "outer horizon", then an "inner horizon", and finally a "ring singularity" inside all those. From the classic book by Hawking and Ellis:
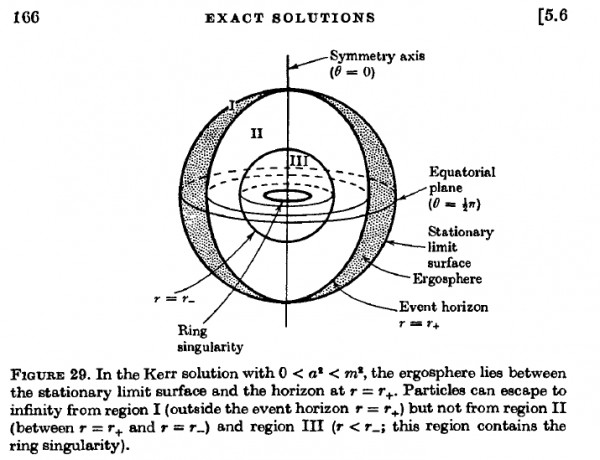
Defining the "size" of these things is a challenge, since the radius of some structure in some arbitrary coordinate system may not have much physical meaning: it's a curved spacetime and the Killing vector field describing "time" is not orthogonal to a preferred foliation by surfaces describing "space". But still, someone should have tried to define and compute the "size" of these various things. What answers did they get?
I'm actually even more interested in the case where
q2+a2>m2
In this case there is a naked ring singularity. Still there should be some ways to define a "size".
 Q&A (4908)
Q&A (4908) Reviews (205)
Reviews (205) Meta (440)
Meta (440) Q&A (4908)
Q&A (4908) Reviews (205)
Reviews (205) Meta (440)
Meta (440)