

Then, we must to prove that
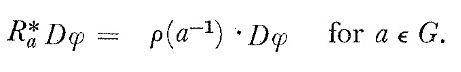
The proof is as follows:
$$R_{a}^{*} D \phi (X,Y)= D \phi (R_{a *} X , R_{a *} Y)=( (d \phi ) h) (R_{a *} X , R_{a *} Y) $$
$$R_{a}^{*} D \phi (X,Y)=d \phi( h(R_{a *} X),h(R_{a *} Y) )=d \phi( (h \circ R_{a *} )(X) , (h \circ R_{a *} )(Y) ) ) $$
Using that
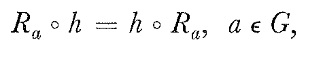
we obtain
$$R_{a}^{*} D \phi (X,Y)=d \phi( ( R_{a *} \circ h )(X) , ( R_{a *} \circ h )(Y) ) ) =d \phi( R_{a *} ( h (X) ), R_{a *} (h (Y) )) ) $$
it is to say
$$R_{a}^{*} D \phi (X,Y) = R_{a}^{*} d\phi (h(X),h(Y)) = (R_{a}^{*} \circ d)(\phi (h(X),h(Y)) ) $$
Now using
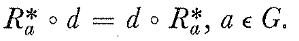
We obtain
$$R_{a}^{*} D \phi (X,Y) = ( d \circ R_{a}^{*} )(\phi (h(X),h(Y)) ) = d ( R_{a}^{*} \phi (h(X),h(Y)))$$
Finally, using
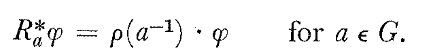
we obtain
$$R_{a}^{*} D \phi (X,Y) = d ( \rho \left( a ^{-1} \right) \phi (h(X),h(Y))) =\rho \left( a ^{-1} \right) d \phi (h(X),h(Y))$$
$$R_{a}^{*} D \phi (X,Y) = \rho \left( a ^{-1} \right) D \phi (X,Y) $$
it is to say
$$R_{a}^{*} D \phi = \rho \left( a ^{-1} \right) D \phi $$
 Q&A (4871)
Q&A (4871) Reviews (203)
Reviews (203) Meta (439)
Meta (439) Q&A (4871)
Q&A (4871) Reviews (203)
Reviews (203) Meta (439)
Meta (439)