This is a question that has been bothering for a while. I don't know if my answer is correct or not, but anyone look over it?
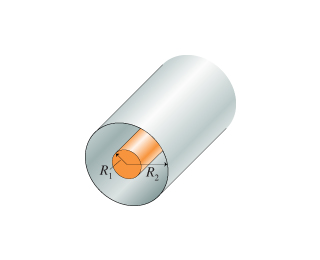
Both cylinders have the same length L. The first cylinder with radius R1 has a charge Q1 uniformly distributed inside the cylinder. The second cylinder is a conductor with radius R2 and charge Q2 (negative) uniformly distributed into the area between the first and second cylinder.
Find the electric field when:
a) r < R1 ; b) R1< r< R2; c) r> R2
So, I did it like this.
a) r< R1
$∮ E.dA = E2πrL = Qi/ε₀ $
$ Qi= ρV= [Q1/(πLR1^2)]*πLr^2 $
$E= rQ1/(2πLε₀R1^2) $
b) R1< r < R2
$∮ E.dA = E2πrL = Qi/ε₀ $
$E= Q1/ (2πrLε₀)$
c) r> R2
$ E1= Q1/ (2πrLε₀) and E2= -Q2/ (2πrLε₀)$ (because Q2 is negative I put the minus in front of it)
$ Eout = E1 + E2 = Q1/ (2πrLε₀) -Q2/ (2πrLε₀) $
 Q&A (4895)
Q&A (4895) Reviews (204)
Reviews (204) Meta (439)
Meta (439) Q&A (4895)
Q&A (4895) Reviews (204)
Reviews (204) Meta (439)
Meta (439)