Physical applications of Adams Operations

Question

Please consider the following theorem extracted from "Fibre Bundles" by Dale Husemoller:

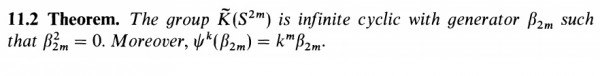
This theorem is formulated in the context  of the Adams operations for K-theory:

 

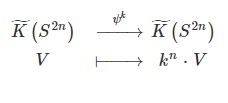
Using Dirac notation we can write:

$$ {\Psi}^{k} | \beta_{{2\,m}} \rangle=  k^{m} | \beta_{{2\,m}} \rangle $$

it is to say,  $| \beta_{{2\,m}} \rangle $ is an eigenvector of eigenvalue $ k^{m} $ for the Adams operations $ {\Psi}^{k}$  on   $ \tilde{K}(S^{2m})$ .

A simple formal proof is as follows

$$ {\Psi}^{k} | \beta_{{2\,m}} \rangle= {\Psi}^{k} [ | a_{1} \rangle \otimes | a_{2} \rangle \otimes... \otimes| a_{m} \rangle ]=  ( {\Psi}^{k}  | a_{1} \rangle )\otimes( {\Psi}^{k} | a_{2} \rangle) \otimes... \otimes| ( {\Psi}^{k}a_{m} \rangle )$$ 

which is reduced to

$$ {\Psi}^{k} | \beta_{{2\,m}} \rangle=  ( k | a_{1} \rangle )\otimes( k| a_{2} \rangle) \otimes... \otimes(|  ka_{m} \rangle )=k^{m} [ | a_{1} \rangle \otimes | a_{2} \rangle \otimes... \otimes| a_{m} \rangle ]$$ 

and then

$$ {\Psi}^{k} | \beta_{{2\,m}} \rangle=   k^{m} | \beta_{{2\,m}} \rangle$$ 

Then, my question is : Do you know any physical application of this theorem?  Many thanks.