Problems while Wick rotating the path integral

Question

I have engaged in the derivation of the Euclidean path integral performing the Wick rotation in full detail. Unfortunately I am facing some trouble and I come here seeking advice.

For simplicity I work on 1 dimension and in god-given units. The amplitude for a spinless particle of unit mass to go from the point $x_i$ to the point $x_f$ in a time interval $T$  is given by
$$
\int D[x]\,e^{i\int_0^Tdt\,\mathcal{L}(t)}
$$
$$
=\int D[x]\,e^{i\int_0^Tdt\,\big\{\frac{1}{2}\left(\frac{dx}{dt}\right)^2-V(x)\big\}}
$$
let's focus on the integral on the exponent
$$
\int_0^Tdt\,\big\{\frac{1}{2}\left(\frac{dx}{dt}\right)^2-V(x)\big\}
$$
to get the Euclidean path integral i gotta Wick-rotate this. In order to do this i write the Lagrangian for a general complex variable $z=t+i\beta$
$$
\mathcal{L}(z)=\frac{1}{2}\left(\frac{dx}{dz}\right)^2-V(x(z))
$$
and I consider the contour

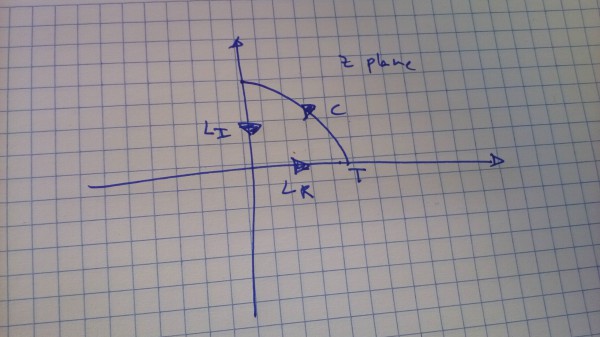
I also assume (maybe naively) that there is no pole in bothering us for $\mathcal{L}(z)$. Cauchy's theorem allows us to write
$$
\int_{L_R}dz\,\mathcal{L}(z)+\int_{L_I}dz\,\mathcal{L}(z)+\int_{C}dz\,\mathcal{L}(z)=0
$$
Let's go one by one. For $L_R$ I parametrize $z(t)=t$
$$
\int_{L_R}dz\,\mathcal{L}(z)=\int_0^Tdt\,\big\{\frac{1}{2}\left(\frac{dx}{dt}\right)^2-V(x)\big\}
$$
For $L_I$ I have $z(\beta)=i\beta$
$$
\int_{L_I}dz\,\mathcal{L}(z)=-i\int_0^Td\beta\,\big\{\frac{1}{2}\left(\frac{dx}{id\beta}\right)^2-V(x)\big\}
$$
for $C$ i have $z(\phi)=Te^{i\phi}$
$$
\int_{C}dz\,\mathcal{L}(z)=iT\int_0^{\pi/2}d\phi\,e^{i\phi}\big\{\frac{1}{2}\left(\frac{dx}{iTe^{i\phi}d\phi}\right)^2-V(x)\big\}
$$
by Cauchy's theorem then
$$
\int_0^Tdt\,\big\{\frac{1}{2}\left(\frac{dx}{dt}\right)^2-V(x)\big\}=i\int_0^Td\beta\,\big\{-\frac{1}{2}\left(\frac{dx}{d\beta}\right)^2-V(x)\big\}-\int_{C}dz\,\mathcal{L}(z)
$$
if I plug this in the path integral I get
$$
\int D[x]\,e^{i\int_0^Tdt\,\big\{\frac{1}{2}\left(\frac{dx}{dt}\right)^2-V(x)\big\}}
$$
$$
=\int D[x]\,e^{\int_0^Td\beta\,\big\{\frac{1}{2}\left(\frac{dx}{d\beta}\right)^2+V(x)\big\}}e^{-i\int_{C}dz\,\mathcal{L}(z)}
$$
and you see the problem here. I lack a minus sign in the first exponential, and the second one shouldn't be there. Maybe I can get the correct expression by manipulating the second exponential but I right now I don't see how. Can anyone right my wrongs?