Question

Looking for references to multiple bounce solutions for Friedmann equations using Klein-Gordon scalar field.

Comments

Can anyone point me to a reference for multiple-bounce solutions for this simple model?

Answer 1

This is my answer, but I've not found other descriptions of this simple model.

The Klein-Gordon wave equation of motion in the Robertson-Walker (RW) metric with scale factor $a(t)$ as a function of time,

$$\begin{array}{*{20}{c}} { - 1,}&{\frac{{{a^2}(t)}}{{1 - K{r^2}}},}&{{a^2}(t){r^2},}&{{a^2}(t){r^2}{{\sin }^2}\theta } \end{array}$$ is

$$\psi ''(t) = - 3H(t)\psi '(t) - {\omega ^2}\psi (t)$$

where $H(t)$is the Hubble parameter defined in terms of the scale factor.

$$H\left( t \right) = \frac{{\dot a\left( t \right)}}{{a\left( t \right)}}$$

and the constant frequency with units ${\text{secon}}{{\text{d}}^{ - 1}}$,

$\omega = \frac{{{{\text{M}}_{KG}}{{\text{c}}^2}}}{\hbar }$

The canonical energy-momentum tensor for the KG wave equation is diagonal with two independent components (0,0), (1,1) which are the matter and pressure energy density.

$\mu = \hbar {\omega ^{ - 1}}{\psi '^*}\psi ' + {{\text{M}}_{KG}}{{\text{c}}^2}{\psi ^*}\psi$

$p = \hbar {\omega ^{ - 1}}{\psi '^*}\psi ' - {{\text{M}}_{KG}}{{\text{c}}^2}{\psi ^*}\psi$

The time derivative of the real-valued densities is provided by the KG wave equation.

$\dot \mu = - 3H(p + \mu )$

${\left( {\dot p - \dot \mu } \right)^2} = 4{\omega ^2}\left( {{\mu ^2} - {p^2}} \right)$

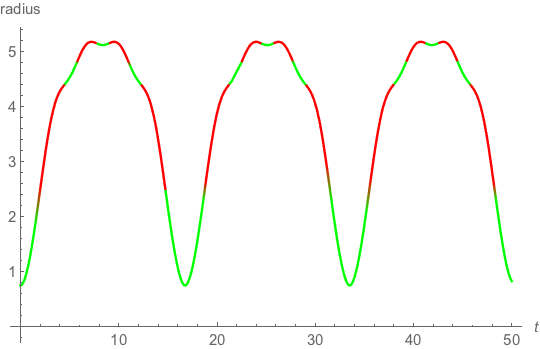
The pressure must go negative to get a bounce, but must be less than the energy density of matter at the same location.

$- 1 \leqslant \frac{p}{\mu } \leqslant - \frac{1}{3}$

The green area is where the pressure is in this negative region.